普段私たちは 0 - 9 までの数字を使う「10進数」という数の体系を使っている。
これに対しコンピューターが計算する時には「2進数」「16進数」などといった、少し違った形で計算をしている。
この2進数や16進数とはなんなのか。また、どのようにして普段使っている10進数以外の数の形を使うことができるのか、説明していく。
そもそもn進数とは?
n進数とは、「一桁にn個集まったら桁が上がる」ことを表す数字のこと。
最も身近に使われている10進数について考えると、「0,1,2,3,4,5,6,7,8,9と10こ集まったら桁が上がる」
と考えることができる。
n進数の具体例
n進数は具体的にどのように使われているだろうか?
お金の数え方は10進数
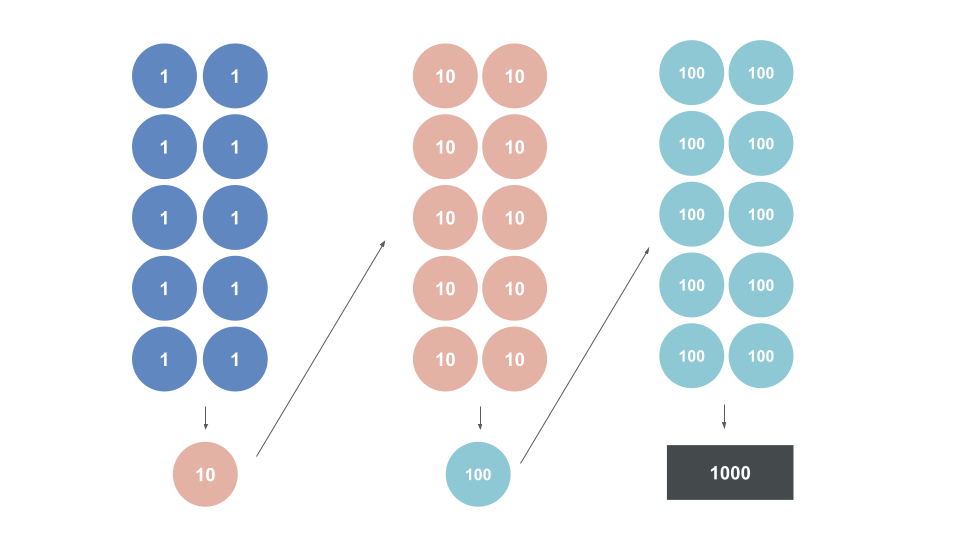
10進数の身近な例としてはお金が挙げられる。
1円が10枚集まれば100円になるし、100円が10枚集まると1000円になる。
時計の進み方は60進数
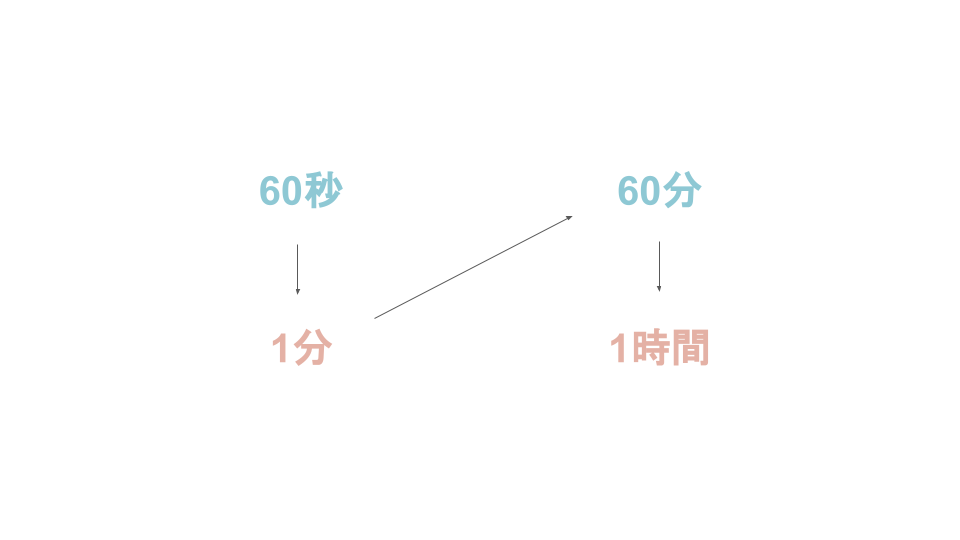
1秒が60集まれば1分になるし、1分が60集まれば1時間になる。
普段私たちは時間を60進数で見ている。
コンピューターでよく使われるn進数
お金や時間などの例を使ってn進数の例を見てきた。
コンピューターでよく使われるn進数として、2進数と16進数が挙げられる。
2進数
2進数は、下の位が、0,1と2個集まったら桁が上がる数になる。
2進数の例
2進数と10進数を比較すると、下記のようになる。
| 2進数 | 10進数 |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | 10 |
なぜ2進数が使われるのか?
コンピューターは電子回路の集まりなので、それぞれの回路で、「電流が流れたら1、電流が流れてなかったら0」という形で情報を受け取る。
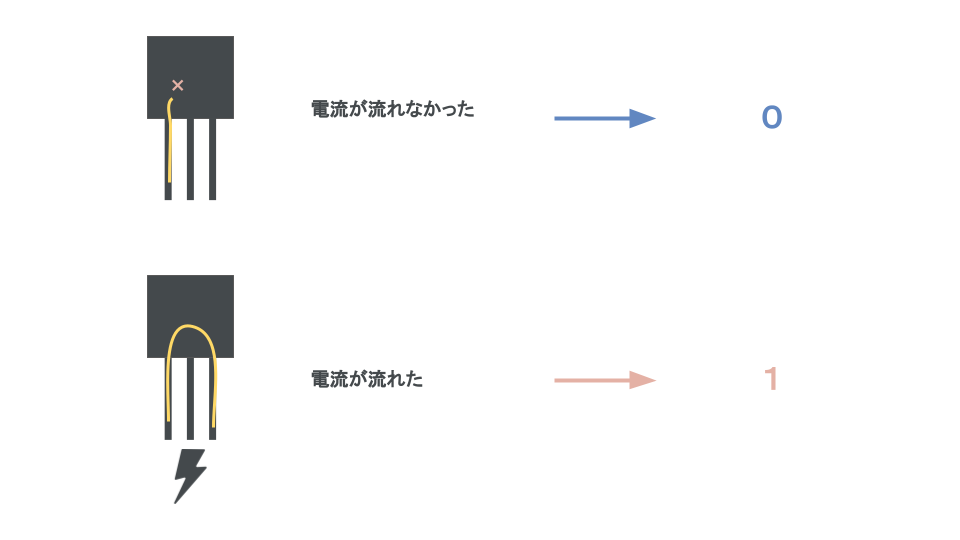
この電子回路で受け取った情報「1」と「0」を使って計算するのに相性の良い方法として2進数が使われるようになった。
詳しくは下記に書いた。
-
-
ビット(bit)とは?ビットによる文字表現や画像、音のデジタル化を解説
ビット(bit)とは何か説明する。 bitの略語元となっている、binary digit (2進数)に関しても合わせて解説。 ASCIIコードによる文字表現や画像、音がどのようにビット表現され、デジタ ...
続きを見る
16進数
16進数は、下の位が、0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15と16個集まったら桁が上がる数になる。
コンピューターの分野では、0から16までの数字の代わりに、0から9までの数字と英字のA, B, C, D, E, Fが使われる。
16進数の例
以下は2進数、10進数、16進数を比較した表になる。
| 2進数 | 10進数 | 16進数 |
| 00000000 | 0 | 0 |
| 00000001 | 1 | 1 |
| 00000010 | 2 | 2 |
| 00000011 | 3 | 3 |
| 00000100 | 4 | 4 |
| 00000101 | 5 | 5 |
| 00000110 | 6 | 6 |
| 00000111 | 7 | 7 |
| 00001000 | 8 | 8 |
| 00001001 | 9 | 9 |
| 00001010 | 10 | a |
| 00001011 | 11 | b |
| 00001100 | 12 | c |
| 00001101 | 13 | d |
| 00001110 | 14 | e |
| 00001111 | 15 | f |
| 00010000 | 16 | 10 |
16進数を使うメリット
コンピューターは基本的に2進数で計算すると説明したが、2進数だけで計算をすると、桁数が長くなりがちになる。
16進数によって二進数を短く表現することで、人間にも分かりやすくなる。
なぜ16進数が相性がいいの?
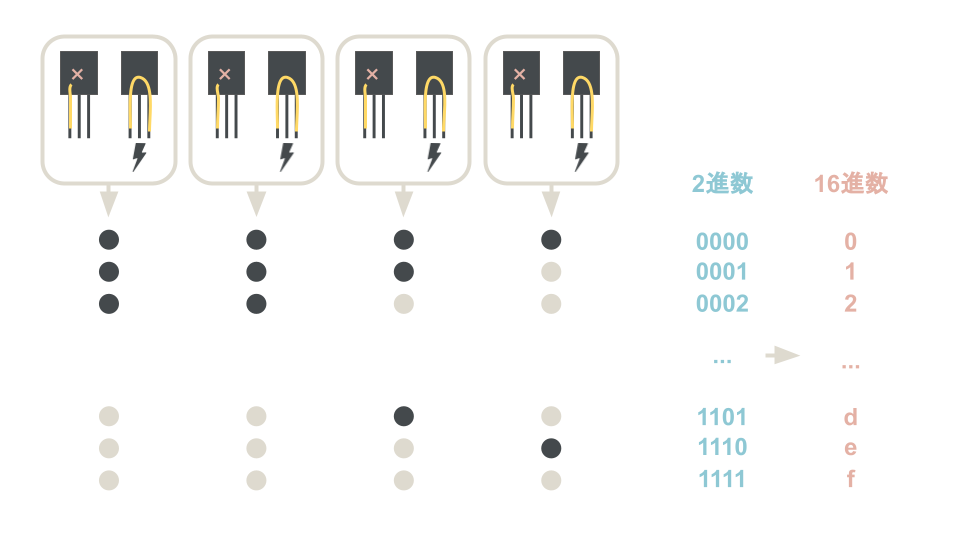
16進数の一つの桁の範囲である0 - 15 を二進数で表すと 0000 - 1111 と表現でき、2進数の4桁分の数字を16進数で1桁で表現できるから。
8進数も、一つの桁の範囲である0 - 7を2進数000 - 111と表すことができるため、2進数の3桁分の数字を1桁で表現できるが、現在は16進数が主流で使われている。
基数とは
n進数には「基数」という概念があり、位が変わる時の基準となる数を表している。
例えば、富士山の高さ3,776.12mを位ごとに表す。
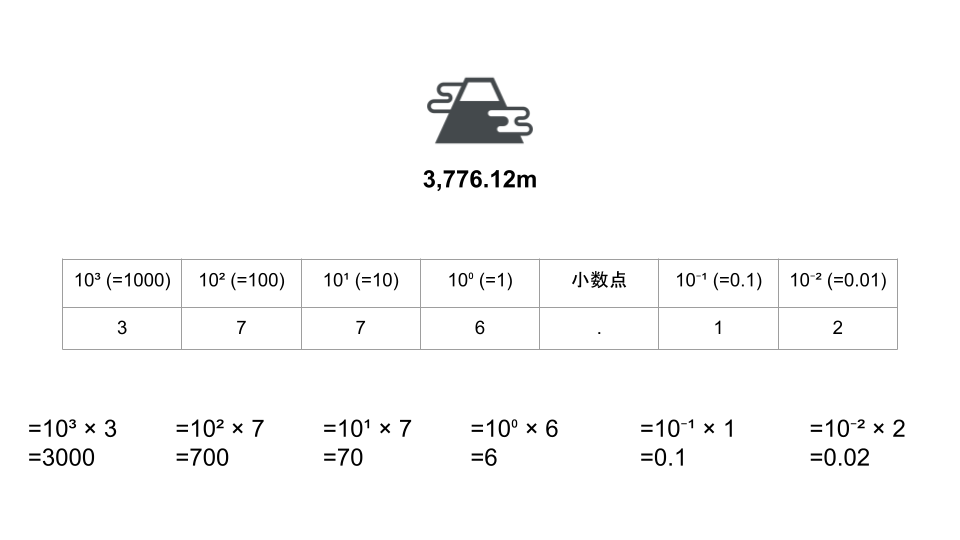
という風に位を考えることができる。
専門用語として、基数、重みという言葉がある。
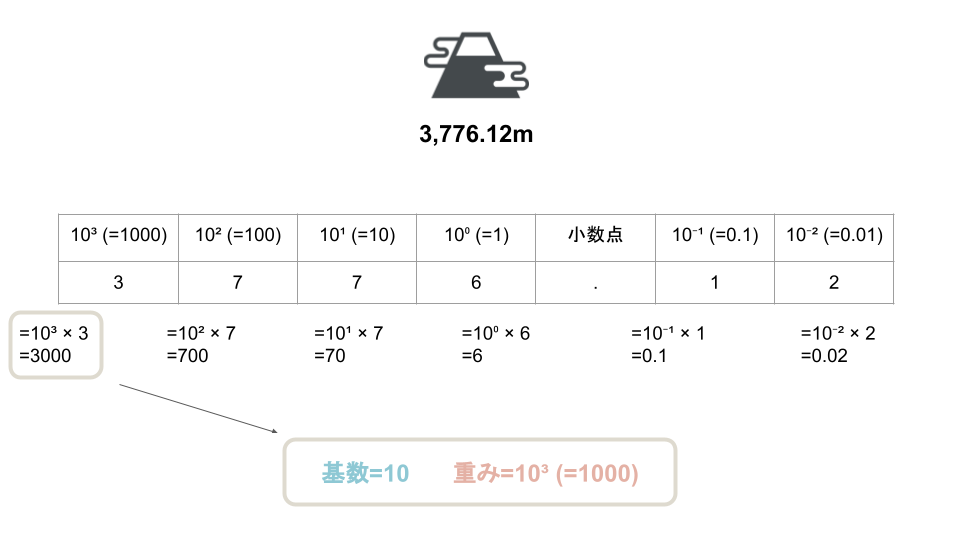
例えば10³ × 3の部分を例に取ると
- 基数:10(位が変わる時の基準)
- 重み:10³(基数を累乗した数。10³ = 1000)
となる。
n進数の重みを比較
2進数、10進数、16進数の重みを比較すると下記の通り。
| 3 | 2 | 1 | 0 | 小数点 | -1 | -2 | |
| 10進数 | 10³ (=1000) | 10² (=100) | 10¹ (=10) | 10⁰ (=1) | . | 10⁻¹ (= 1/10 = 0.1) | 10⁻² (= 1/100 = 0.01) |
| 2進数 | 2³ (=8) | 2² (=4) | 2¹ (=2) | 2⁰ (=1) | . | 2⁻¹ (= 1/2 = 0.5) | 2⁻² (= 1/4 = 0.25) |
| 16進数 | 16³ (=4096) | 16² (=256) | 16¹ (=16) | 16⁰ (=1) | . | 16⁻¹ (= 1/16 = 0.0625) | 16⁻² (= 1/256 ≈ 0.0039) |
| n進数 | n³ | n² | n¹ | n⁰ | . | n⁻¹ | n⁻² |
二進数だけの計算だと、桁が長くなり過ぎてしまい、人間が読み取るにはとても難しくなってしまう。
なので2進数⇄10進数⇄16進数⇄その他必要に合わせてn進数を変換する作業を行うことで、必要な基数を使って計算を行うことができる。
基数変換
2進数から10・16進数に変えたり、16進数から2・10進数に変換するなど、基数を変換するにはどのようにしたら良いだろうか。
n進数→10進数
例として、5進数の123.21を10進数に変換する。
変換するときは、それぞれの重みに桁ごとの数字を当てはめていく。
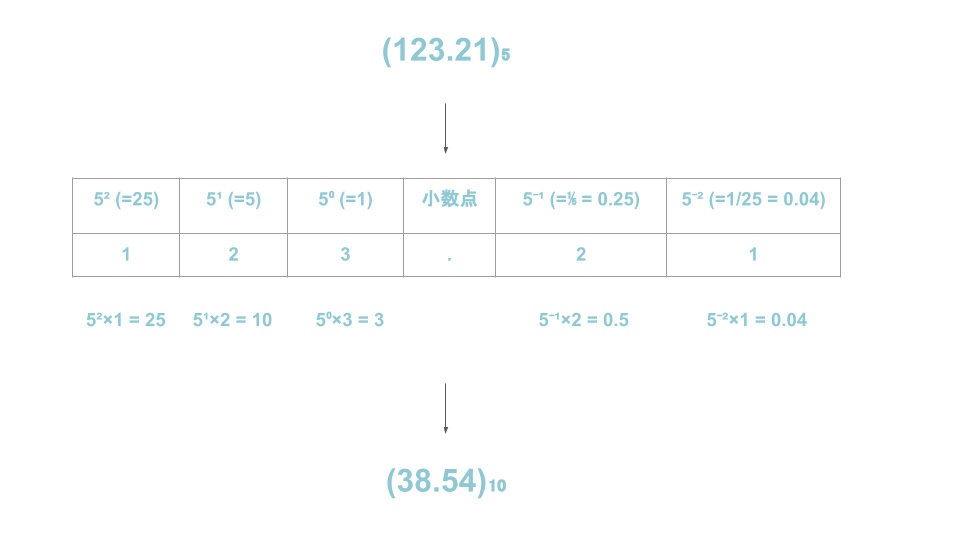
10進数→n進数
例として、10進数の40を5進数に変換する。
10進数から変換する際は、割り算を行うことで、変換することができる。
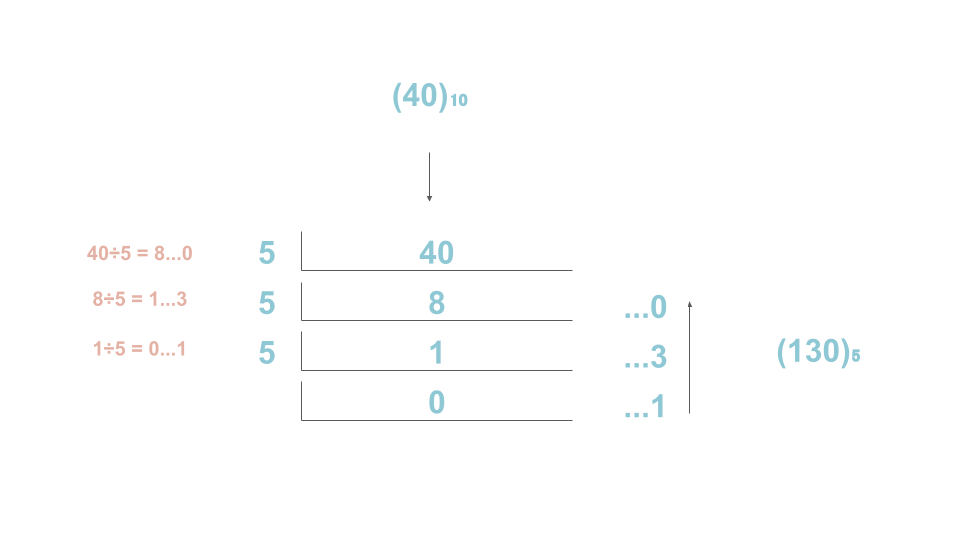
割り算した結果の余りの部分がn進数で変換された数字となる。
今回の例なら10進数の40は5進数では130となった。
2進数→16進数
2進数の01111011を16進数に変換する場合は、4桁ごとに数字を区切ることで、変換が簡単になる。
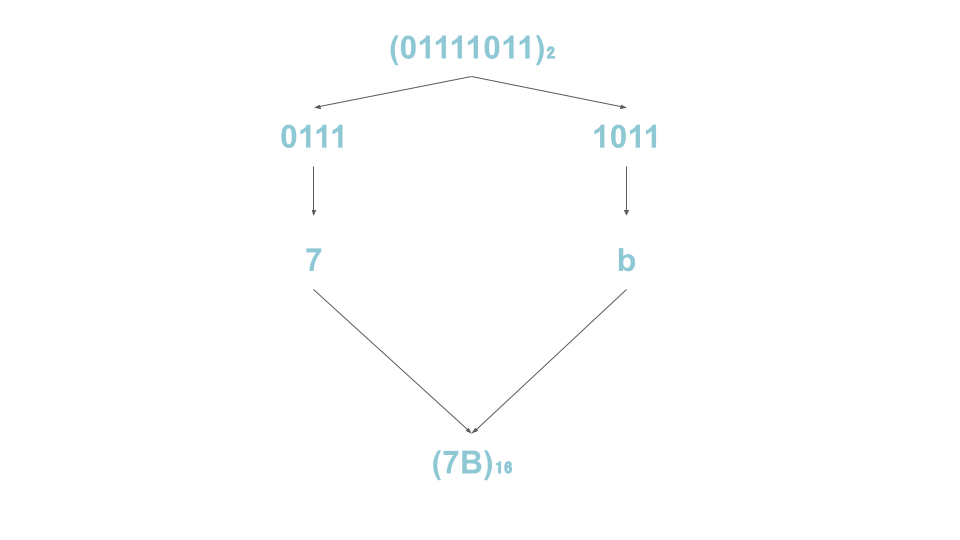
16進数→2進数
16進数の4Fを2進数に変換する際も、16進数の各桁を2進数4桁にばらすことで変換できる。

コンピュータの全体像
コンピュータの全体像を知ると、数学とコンピューターサイエンスの結びつき方もより深く理解できる。
こちらにコンピューターサイエンスの全体像についてまとめた。
-

-
Screen-Shot-2021-06-11-at-11.45.16
続きを見る