ITにおいて重要なアルゴリズムとは何か説明する。
また、日常生活や普段私たちが使っているWebサービスでどのようにアルゴリズムが使われているか紹介する。
サーチアルゴリズム(探索アルゴリズム)、ソートアルゴリズム(整列アルゴリズム)などの実際のアルゴリズムも図と合わせて紹介する。
アルゴリズムとは?
アルゴリズムとは、問題を解決するための効率的な手順。
なぜアルゴリズムが重要なのか?
より良いアルゴリズムを考えることは、より早く、効率的に問題を解決することができることにつながるから。
日常生活のアルゴリズムの具体例
アルゴリズムは問題を解決するための効率的な手順と説明したが、ここでいう問題や手順とは何を指すのだろう?
日常生活の例をここで出してみる。
いちょう切り
例えば料理でなるべく時短で済ませたいとする。色々時短の方法を見つける中で、野菜の切り方に注目する。
野菜をいちょう切りで準備する時、どんな手順で切ったら一番手順が少なく済むだろうか?これがアルゴリズムの問題となる。

ではどんな手順で切ったら一番少ない回数で済むだろうか。
ここでは2通りの方法を比較してみる。
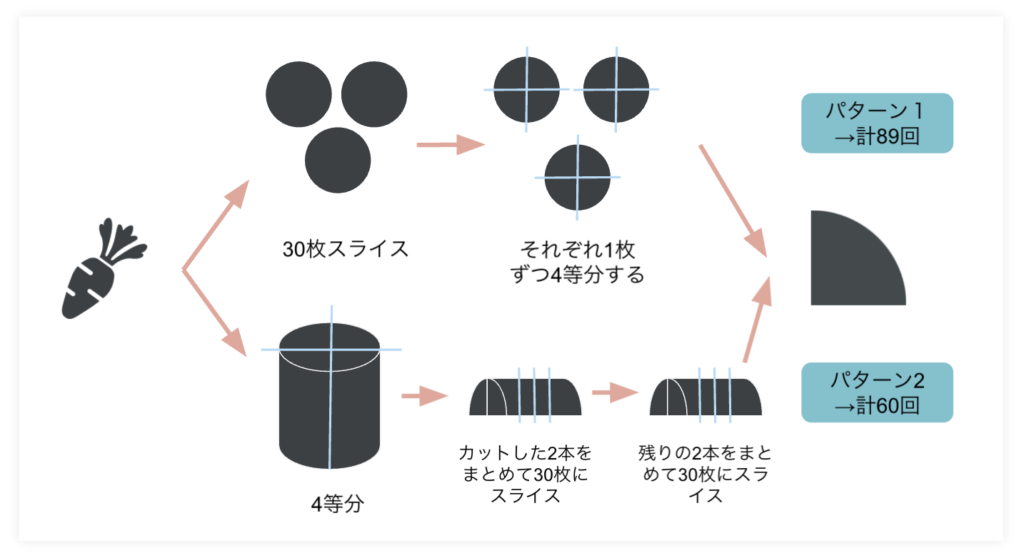
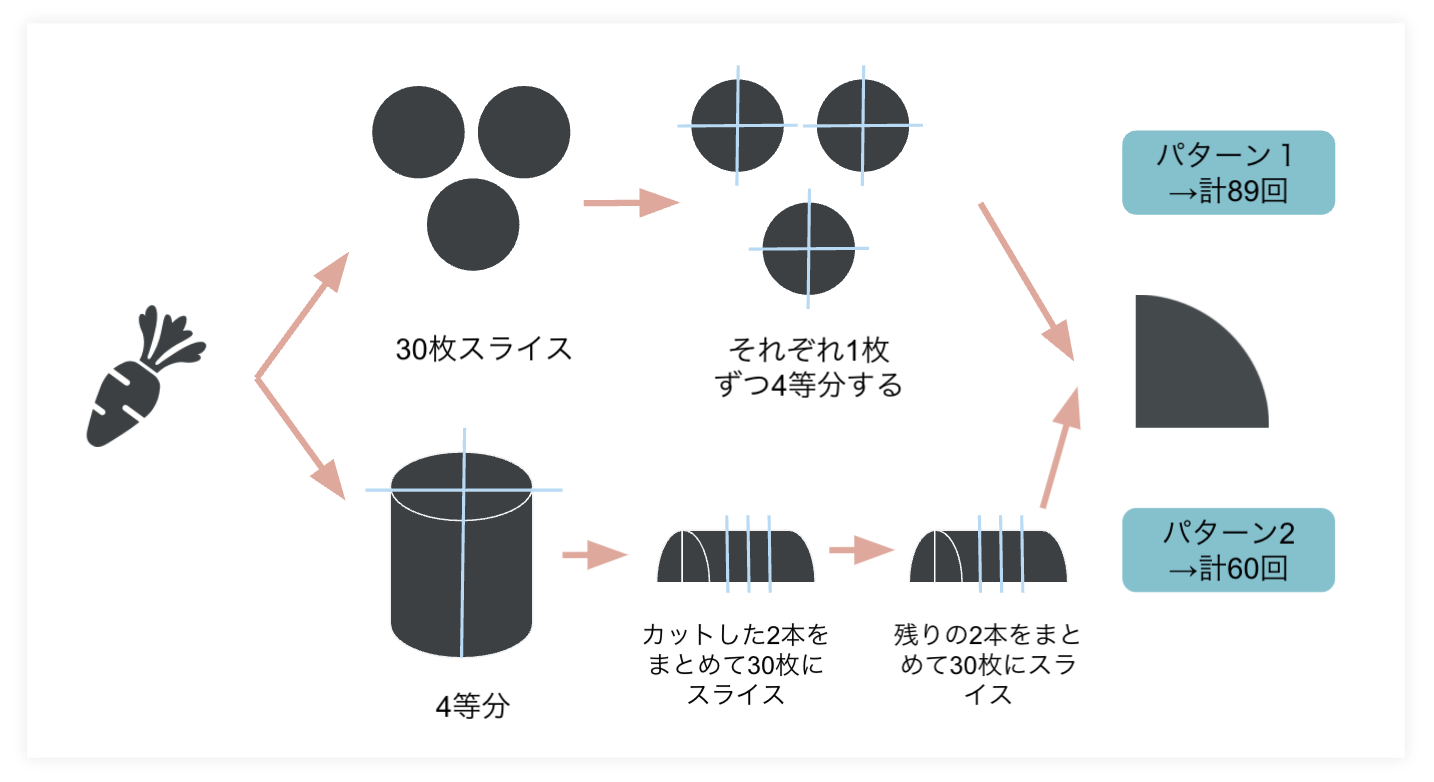
パターン1の場合:
- にんじんを30枚にスライス(29回)
- 1枚ずつ4等分にカット(30枚×2回カット=60回カット)
合計89回カットした。
パターン2の場合:
- 4等分にカット(2回)
- 4等分のうち二つをまとめてスライス(29回カット)
- 残った二つもまとめてスライス(29回カット)
合計60回カットした。
カット数を比較すると、パターン2で切った方が効率的にいちょう切りができていることがわかる。
辞書
例えば、辞書で「ら」のキーワードを見つけたいとする。
すると手順としては、ふた通り考えられる。
- 1ページ目から順番にめくっていく
- 辞書を半分ずつめくっていく
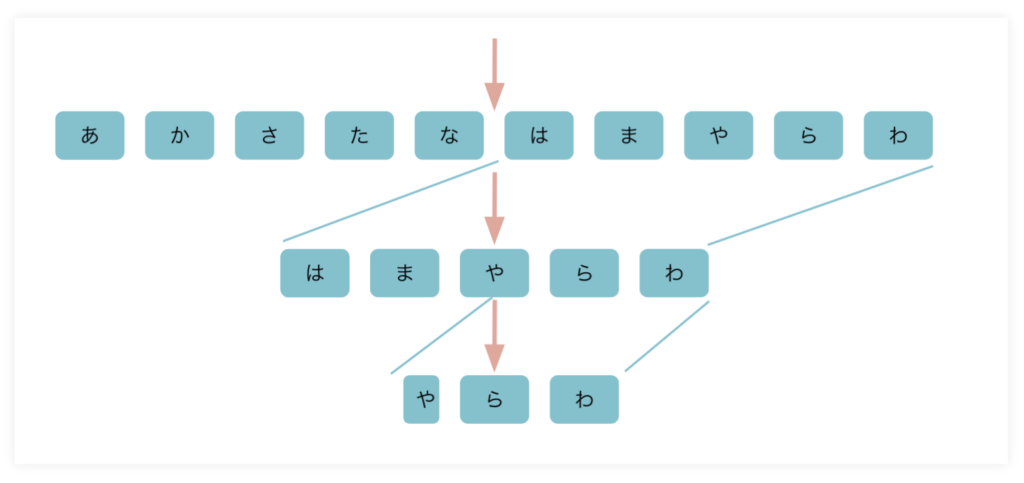
1ページ目から順番にめくっていくよりも、半分ずつめくっていく方が効率的にらのキーワードを見つけられる。
Webサービスで使われている具体例
現在あるWebサービスも、アルゴリズムのおかげでどんどん便利なサービスに進化している。
GoogleやBingなどの検索エンジン

膨大なWebページの中から、ユーザーの検索意図に沿ったページがすぐに表示されるようにアルゴリズムが使われている。
もしアルゴリズムがなければ、辞書を1ページ目から引くように、膨大な時間をかけてページを検索することになってしまう。
SNS

過去の閲覧の履歴、投稿やコメント、いいねなどの機能の活用の履歴、友人関係などの情報をもとにしてどんな投稿をニュースフィードに優先的に表示させるかなど、アルゴリズムを活用している。
よりユーザーにとって使いやすく、長く注意を引いてもらえるようにアルゴリズムを活用している。
乗り換え案内やGoogle Map
A地点からB地点に行く時、どの道が最短経路かなどを導き出す時に、アルゴリズムが使われる。
代表的なアルゴリズムの例
アルゴリズムは様々な種類があり、問題をどのように素早く効率的に解決するかによって使われるアルゴリズムが異なる。
適切なアルゴリズムを選び、効率的にデータを処理できれば、例えばGoogleならより早くユーザーが適切なページを検索できるようになるし、乗り換え案内やマップならその人の条件に合ったより適切なルートを導き出せる。
なので問題に対し、どのようなアルゴリズムを選んで解決するかがとても重要になる。
いくつかアルゴリズムの例を紹介する。
サーチアルゴリズム(探索アルゴリズム)
サーチアルゴリズムは、膨大なデータの中から目的のデータを探し出すために使われる方法。
大きく分けてリニアサーチ(線形探索法)とバイナリーサーチ(二分探索法)が使われる。
リニアサーチ(線形探索法)
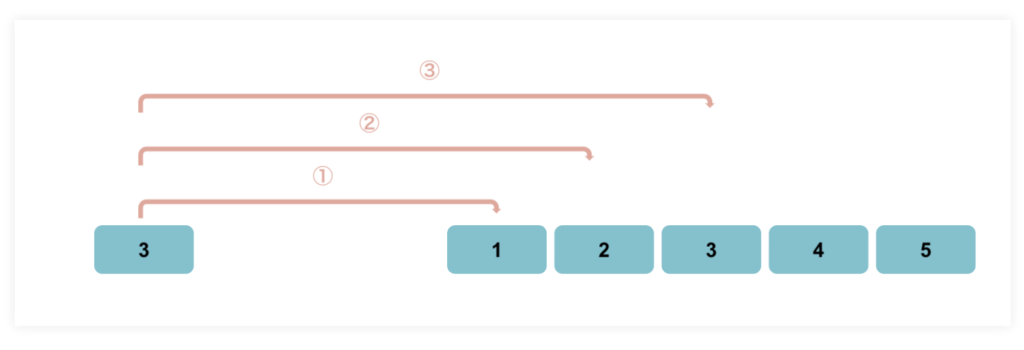
端から順番に目的の情報を探していく方法。
バイナリーサーチ(二分探索法)
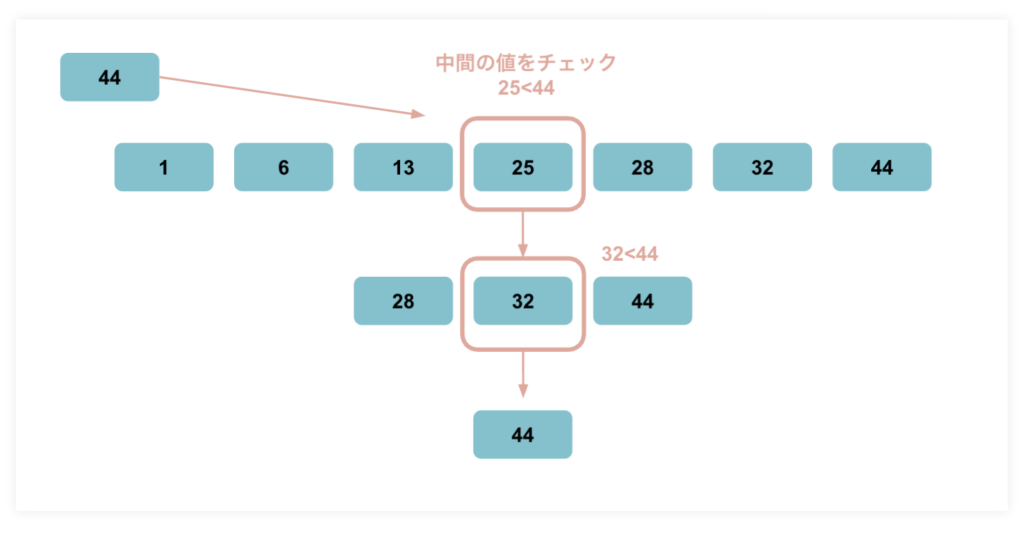
バイナリサーチは羅列されたデータの真ん中から情報を探していく方法。
探しているデータが大きいか小さいかで切り分けていく。
ソートアルゴリズム(整列アルゴリズム)
ソートアルゴリズムは主に大量のデータを一定のルールに沿って並び替えるために使われる方法。
バブルソート
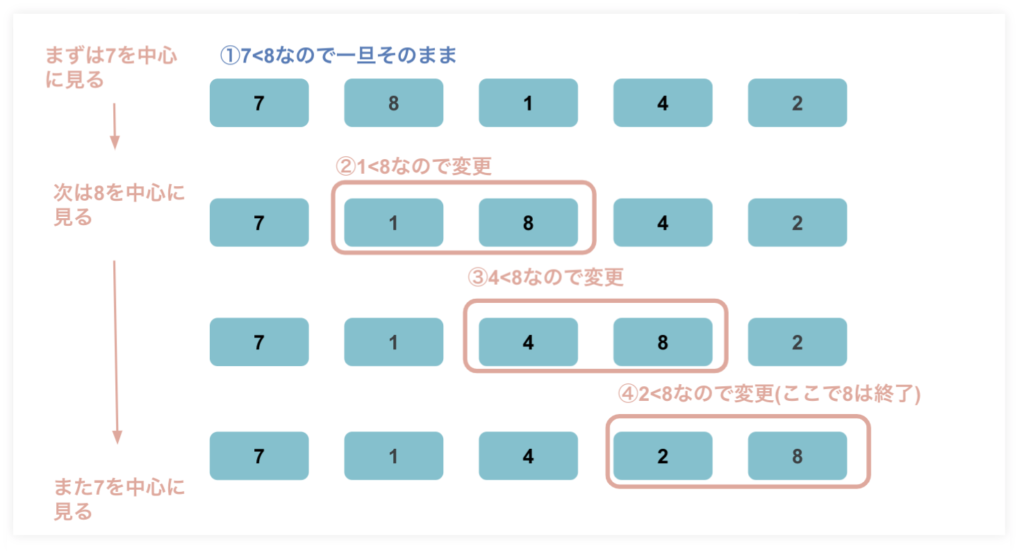
バブルソートは隣の値と比較し、並べ替えていく方法。
画像の例で見ると、
- 1番左の7を中心に見る。
- 隣の8と比較する。8の方が大きいので一旦7の確認は終了
- 次は8を中心に見る。
- 隣の1と比較する。8の方が大きいので順番を変更する。
- 隣の4と比較する。8の方が大きいので順番を変更する。
- 隣の2と比較する。8の方が大きいので順番を変更する。
- 右側に確認する数字がないのでここで終了
- 一番左の7へ戻る
- 隣の1と比較する。7の方が大きいので順番を変更する。
- ...
という流れで、数字が昇順(ここでは1 - 2 - 4 - 7 - 8)になるまでステップを続けていく。
選択ソート
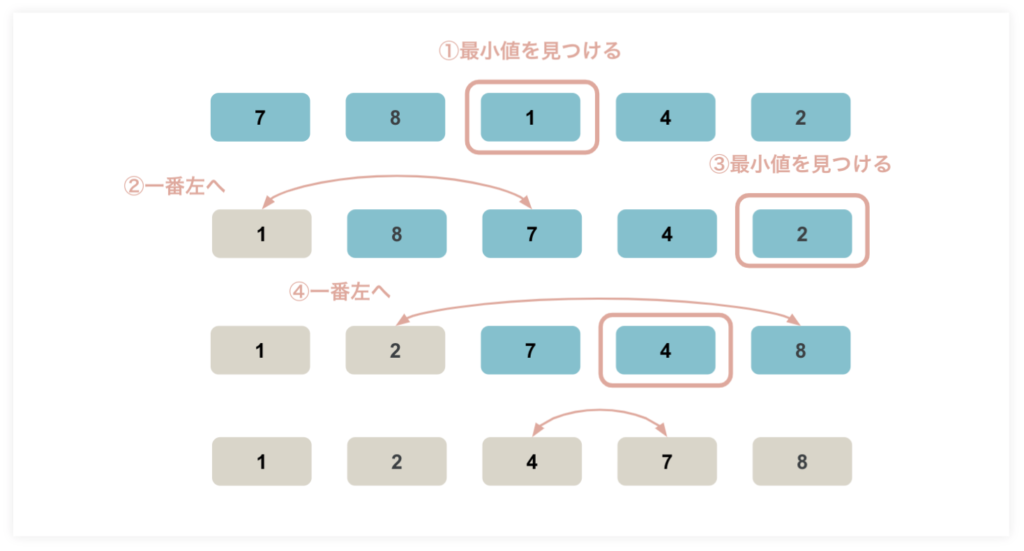
選択ソートはデータの中から最小値もしくは最大値を見つけ、データの一番左に移動させる方法。
- 最小値を見つける
- 一番左へ移動させる
- 残った数字の中で最小値を見つける
- 残った数字の中で一番左へ移す
- ...
を繰り返す。
挿入ソート
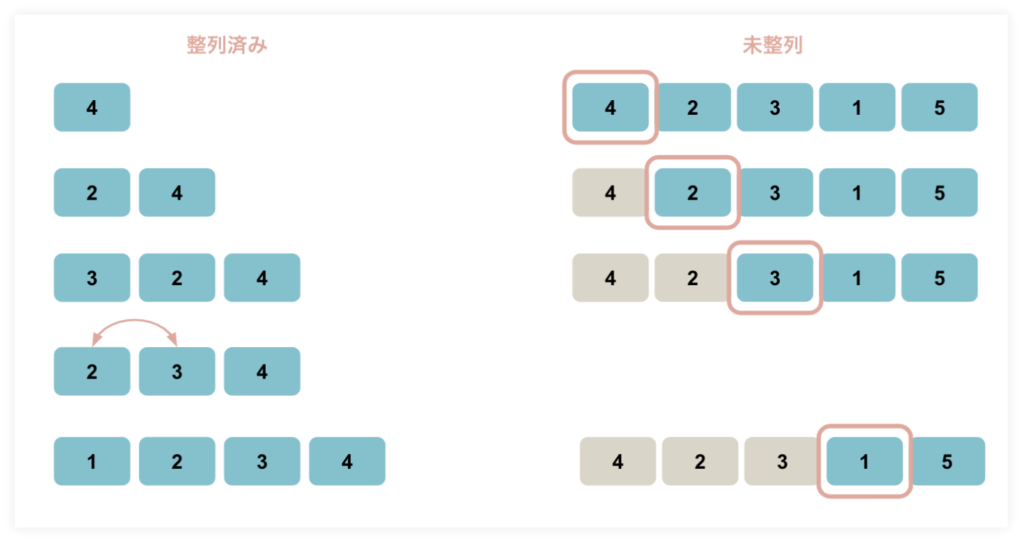
挿入ソートでは、未整列のデータから値を一つづつ取り出していき、整列済みのデータの列に加えていく方法。
整列済みのデータの列にはデータを左端から入れていき、必要であれば並び替えを行う。
画像の例で見ると
- 「未整列の列」の4を「整列済みの列」の左端へ移動
- 「未整列の列」の2を「整列済みの列」の左端へ移動
- 「未整列の列」の3を「整列済みの列」の左端へ移動
- 3と隣の数字の2を比較
- 3の方が大きいので、右側へ移動
- 3と4を比較
- 4の方が大きいのでそのまま
- 「未整列の列」の1を「整列済みの列」の左端へ移動
- ...
という形で「整列済みの列」の数字が昇順に並び替えられるまで続ける。
シェルソート
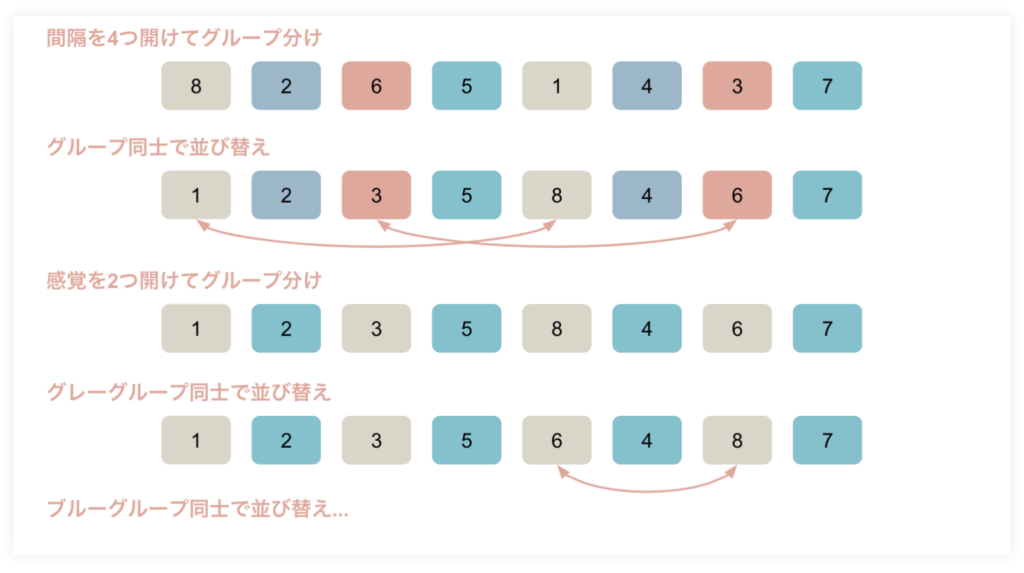
シェルソートは一定間隔でグループを作り、グループごとに並び替えを行っていく方法。
画像の例でいくと
- 一定間隔を4つ作りグループ分け
- グループ同士で並び替え
- 一定間隔を2つ作りグループ分け
- グループ同士で並び替え
- 一定間隔が1になったらグループ分けをせずにそのまま順番を並び替え
という流れになる。
クイックソート
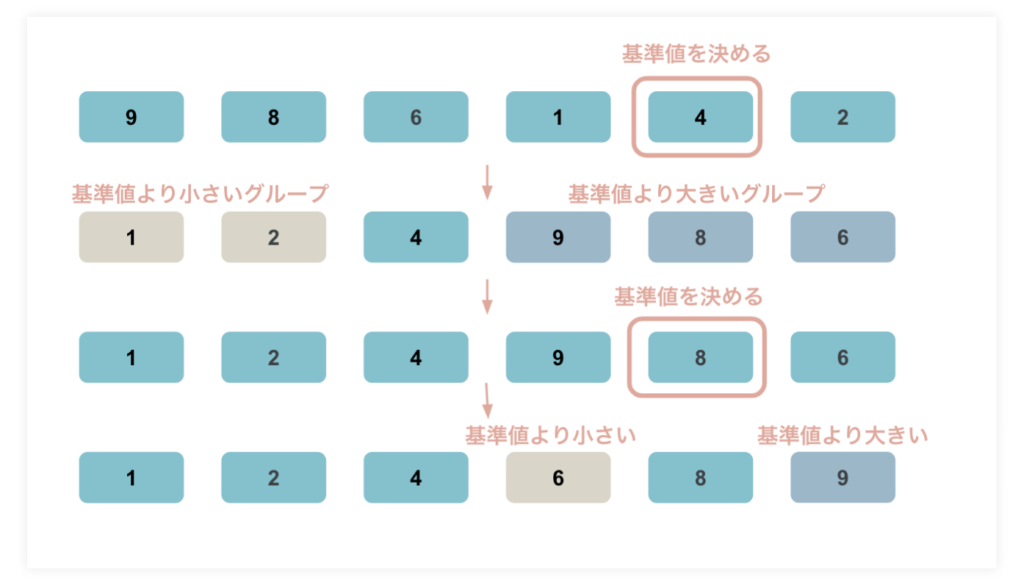
クイックソートは基準値を決めて、基準値より小さいグループと基準値より大きいグループを振り分けて並び替える方法。
マージソート
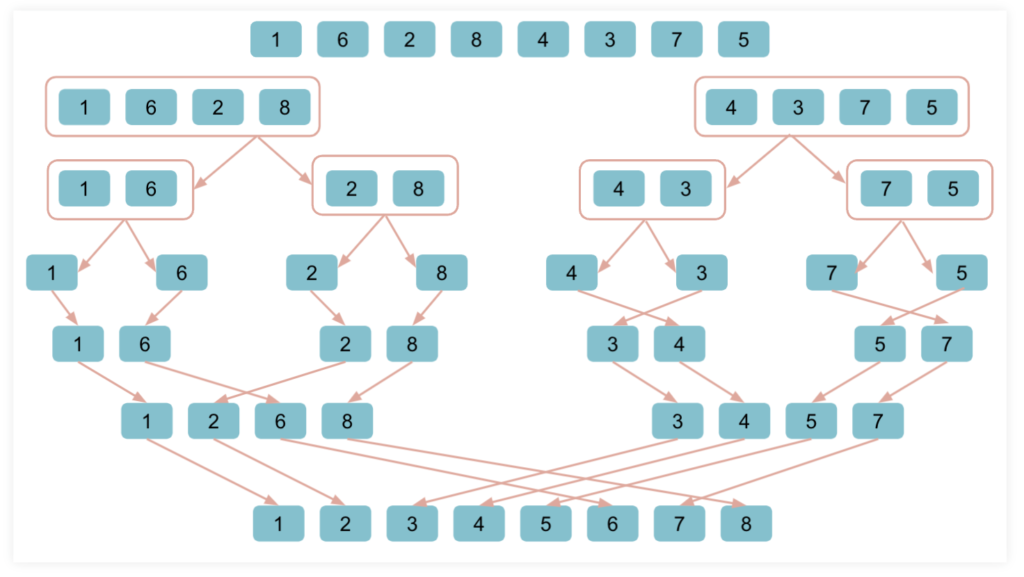
マージソートはデータを一度分割し、分割したデータを並び替えながら再度繋げていく方法。
アルゴリズムの研究はコンピュータ科学の核心
ある作業を行うマシンを構築できるのは、その作業を実行するアルゴリズムが存在するときだけだ。つまり問題を解くアルゴリズムが存在しないならば、その問題の解は、マシンの能力をこえたところにあるといえる。
J.Glenn Brookshear,神林 靖,長尾 高弘. 入門 コンピュータ科学 ITを支える技術と理論の基礎知識 (Japanese Edition) (Kindle Locations 516). Kindle Edition.
引用の通り、アルゴリズムがどんな問題を解決できるのか、どこまで有用なのかを知ることで、マシンの問題解決のレベルを知ることができる。
そのため、コンピュータ科学にとってアルゴリズムの研究はとても重要なものとされている。
特にアルゴリズムがどこまで使えるのか限界を知ることに関しては、1930年代にクルト・ゲーデルが「不完全性定理」という定理を発表。
この定理では、全ての数学理論の中には、アルゴリズムでは解決できないものがあると述べた。
「入門 コンピュータ科学」によればこの不完全性定理の発表を引き継ぐ形で、どこまでアルゴリズムが問題解決に使えるのかの研究が、今日のコンピュータ科学の分野の始まりになったとしている。
この発見は、数学基礎論の世界に激震を走らせた。この研究を引き継ぐ形で始まったアルゴリズムの可能性についての研究が、今日コンピュータ科学として知られる分野の始まりとなったのである。まさにアルゴリズムの研究こそが、コンピュータ科学の核心なのだ。
J.Glenn Brookshear,神林 靖,長尾 高弘. 入門 コンピュータ科学 ITを支える技術と理論の基礎知識 (Japanese Edition) (Kindle Locations 528). Kindle Edition.
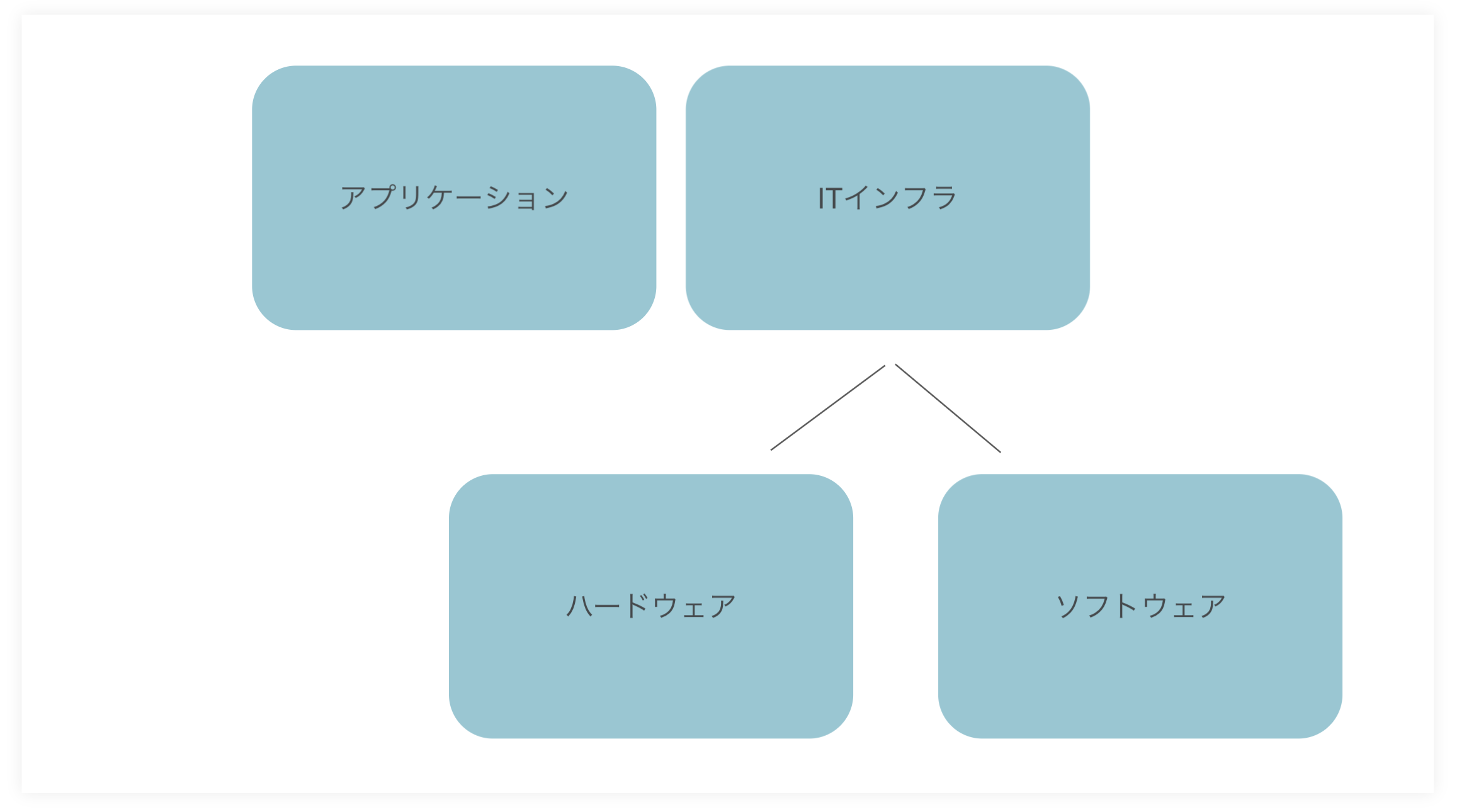
コンピュータの全体像
コンピューターサイエンスにおいてアルゴリズムは核心ともいわれているが、コンピュータの全体像を知るとより理解が深まる。
こちらにコンピューターサイエンスの全体像についてまとめた。
-

-
Screen-Shot-2021-06-11-at-11.45.16
続きを見る