気圧という言葉を聞いたことがあるだろう。天気予報でおなじみの「高気圧」「低気圧」といった現象は、これらの配置が天候を変化させ、雪を生み出す。この気圧を理解するためには「ニュートン」という力の単位について知る必要がある。ニュートンは「力の単位」とよく言われるがどのように気圧や天候に関わっているのか?この記事を通して、ニュートンを起点に降雪に至るまでの旅に出てみたい。
下記は降雪からニュートンの関係性を追った図になる。ニュートンを知ることは気圧とその単位であるパスカル(Pa)の理解に繋がり、降雪の仕組みの理解へとつながっていく。さっそくみていこう。

運動方程式とは〜ニュートンは運動方程式から算出される単位
ニュートン(N)とは何なのか?これを知るにはまず「運動方程式」を知る必要がある。
運動方程式は簡単にいうと、「力を加えたら物がどんな風に動くか」を教えてくれる公式になる。物理の世界を「計算できる形」にして、物の動きをもっと正確に理解するために作られた式だ。
運動方程式を数式で表すと、次のようになる:
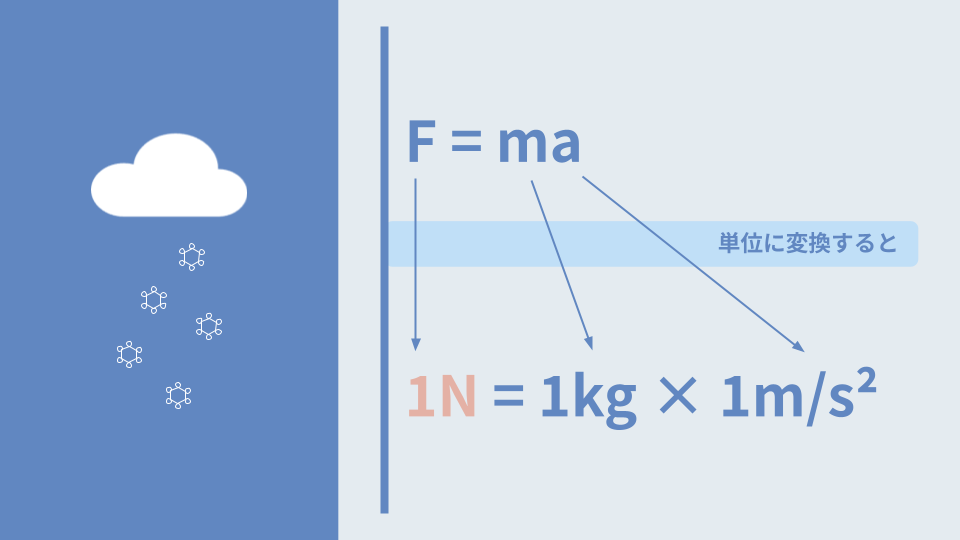
F = ma
- F : 力(Force : 物を押したり引っ張ったりする力)
- m : 質量(mass : 物の「重さ」や「動きにくさ」を表す。重いものほど動かすのが大変)
- a : 加速度(Acceleration : 力を加えると、物が「どれくらい速くなるか」を表す)
この公式によって力が大きいほど加速は大きくなり、質量が大きいほど動きにくいという直感的な現象を、正確な数値で予測することができる。
ニュートン(N)はこの運動方程式の力(Force)を表すための単位として使われている。
ニュートンの定義はこのように表される:
1kgの物体に、1m/s²の加速度を生じさせる力。

ニュートン(N)と気圧の関係〜ニュートンとパスカルの違い
ここまで、力の単位であるニュートンについて見てきたがこれがどう気圧に関係するのか?
ニュートン(N)が登場するのは気圧の計算だ。気圧とはつまり大気の圧力であり、圧力とは単位面積に対して垂直に働く力である。
この大気の圧力はパスカル(Pa)で表すことができ、1Paは1㎡につき1Nの圧力を表している。
1Pa = 1N / ㎡
パスカル(Pa)は圧力の単位であり、ニュートン(N)は力の大きさを表す単位だという区別をすることができる。

1気圧はどのくらいか
1気圧もこのパスカルから計算ができる。気圧の単位で使用するhPa(ヘクトパスカル)は1hpa=100Paとなり、1気圧は1013hPaだ。現実世界での気圧はどのくらいかというと、日本周辺の平均気圧は約1013hPsとされ(1)、富士山頂3776mでは、気圧は約638hPa(2)ほどとなる。
ニュートンは気圧を算出する重要な概念
ニュートンは力を数値化する基本単位であり、その概念は気圧を通じて天候や降雪と深く結びついている。高気圧や低気圧の配置が天候を左右し、降雪をもたらす背景には、ニュートン(N)が深く関わっている。降雪という自然現象も、見えない物理法則の視点から捉えると、単なる天気ではなく、力や気圧が織りなすダイナミックな現象として新たな角度から楽しむことができる。
次は気圧について着目する。
*気圧とは〜低気圧と高気圧の違い、等圧線まで、降雪のメカニズムを探る旅②
雪が降る仕組みについてはこちら。
参照:
(1) 防災システム研究所 - 低気圧と高気圧(ヘクトパスカルとは?)
(2) 気象庁 - 富士山(静岡県) 平年値(年・月ごとの値) 主な要素